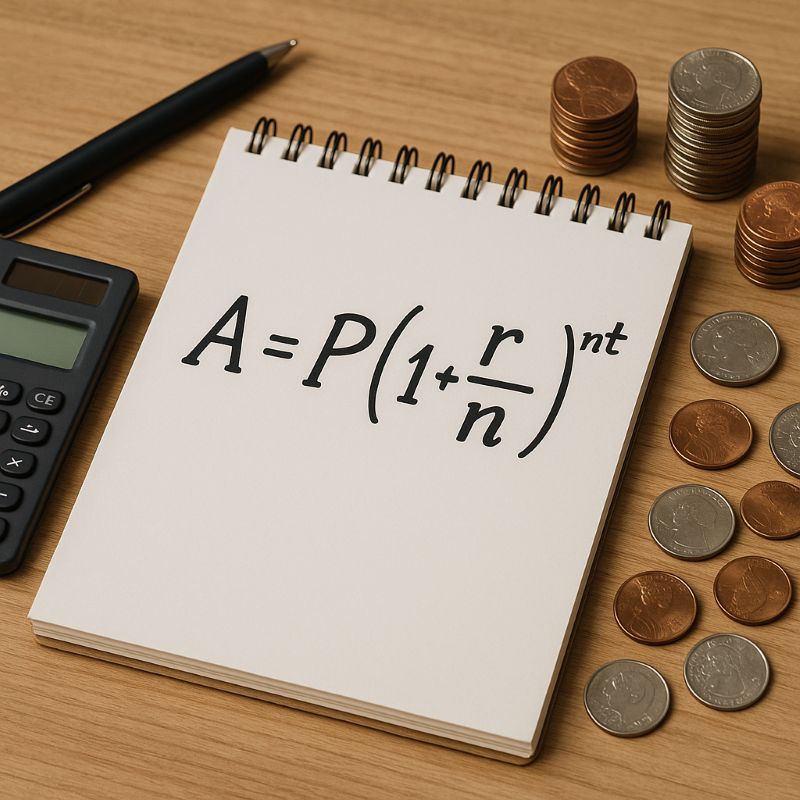Công thức tính lãi kép: hướng dẫn chi tiết và cách áp dụng

Bạn đã bỏ lỡ cơ hội gia tăng tài sản đáng kể vì chưa nắm rõ sức mạnh của lãi kép? Đừng lo lắng! Bài viết này sẽ cung cấp cho bạn công thức tính lãi kép chi tiết và cách áp dụng hiệu quả, giúp bạn khai thác tối đa tiềm năng tài chính của mình. Hãy cùng khám phá ngay!

Lãi kép là gì?

Lãi kép (Compound Interest) là một trong những khái niệm mạnh mẽ nhất trong tài chính, thường được ví von là kỳ quan thứ 8 của thế giới. Hiểu đơn giản, lãi kép là loại lãi được tính không chỉ trên số tiền gốc ban đầu mà còn trên số tiền lãi đã tích lũy từ các kỳ trước đó. Điều này tạo ra một hiệu ứng "lãi chồng lãi", khiến tài sản của bạn tăng trưởng theo cấp số nhân theo thời gian.

Để dễ hình dung, hãy so sánh với lãi đơn. Lãi đơn chỉ được tính trên số tiền gốc ban đầu. Ví dụ, nếu bạn gửi 10 triệu đồng với lãi suất 10% mỗi năm theo hình thức lãi đơn, bạn sẽ nhận được 1 triệu đồng tiền lãi mỗi năm. Tổng số tiền lãi sau 3 năm sẽ là 3 triệu đồng.

Trong khi đó, với lãi kép, số tiền lãi 1 triệu đồng của năm đầu tiên sẽ được cộng vào gốc, và năm thứ hai lãi sẽ được tính trên 11 triệu đồng. Cứ thế, tiền lãi sẽ ngày càng lớn hơn.

Nguyên lý cơ bản của lãi kép là tái đầu tư. Bất kỳ khoản lãi nào kiếm được sẽ được cộng gộp vào vốn gốc, sau đó khoản vốn gốc mới này sẽ tiếp tục sinh lời trong các kỳ tiếp theo. Đây chính là yếu tố làm nên sự khác biệt vượt trội của lãi kép so với lãi đơn.

Qua bảng trên, có thể thấy rõ lợi thế của lãi kép. Sau 3 năm, số tiền bạn nhận được từ lãi kép (13.310.000 VNĐ) cao hơn so với lãi đơn (13.000.000 VNĐ) mặc dù cùng mức lãi suất và thời gian. Đây là lý do tại sao việc hiểu và áp dụng công thức tính lãi kép lại quan trọng đến vậy trong việc xây dựng kế hoạch tài chính cá nhân.

Công thức tính lãi kép

Để có thể khai thác sức mạnh của lãi kép, điều quan trọng nhất là phải nắm vững công thức tính lãi kép chuẩn và hiểu rõ từng thành phần của nó.

Công thức tổng quát tính lãi kép

Công thức tính lãi kép tổng quát được biểu diễn như sau:

A=P×(1+nr​)nt

Trong đó:

• A: Tổng số tiền nhận được trong tương lai (bao gồm cả vốn gốc và lãi). Đây là mục tiêu cuối cùng bạn muốn tính toán.

• P: Số tiền vốn gốc ban đầu (Principal amount) mà bạn đầu tư hoặc gửi tiết kiệm.

• r: Lãi suất danh nghĩa hàng năm (Annual interest rate). Lưu ý rằng lãi suất này phải được biểu diễn dưới dạng số thập phân khi đưa vào công thức tính lãi kép (ví dụ, 8% sẽ là 0.08).

• n: Số lần lãi được ghép trong một năm (Number of times interest is compounded per year). Đây là yếu tố cực kỳ quan trọng, ảnh hưởng lớn đến kết quả cuối cùng. Ví dụ:

• Ghép lãi hàng năm: n=1

• Ghép lãi bán niên (nửa năm một lần): n=2

• Ghép lãi hàng quý: n=4

• Ghép lãi hàng tháng: n=12

• Ghép lãi hàng ngày: n=365

• t: Số năm (Time in years) mà số tiền được đầu tư hoặc gửi tiết kiệm.

Ví dụ thực tế: Giả sử bạn gửi tiết kiệm 10.000.000 VNĐ vào ngân hàng với lãi suất 8% mỗi năm, lãi được tính theo tháng, trong vòng 3 năm. Hãy cùng áp dụng công thức tính lãi kép để xem số tiền bạn nhận được là bao nhiêu:

• P=10.000.000 VNĐ

• r=0.08 (8%)

• n=12 (lãi tính theo tháng)

• t=3 năm

Áp dụng vào công thức tính lãi kép:

A=10.000.000times(1+frac0.0812)(12times3) A=10.000.000times(1+0.00666667)36 A=10.000.000times(1.00666667)36 Aapprox10.000.000times1.270237 Aapprox12.702.370 VNĐ

Vậy, sau 3 năm, bạn sẽ nhận được khoảng 12.702.370 VNĐ.

Minh họa công thức lãi kép với giấy và máy tính bỏ túi

Công thức tính lãi kép đơn giản cho các trường hợp đặc biệt

Mặc dù công thức tính lãi kép tổng quát có thể áp dụng cho mọi trường hợp, nhưng trong một số tình huống cụ thể, bạn có thể sử dụng các biến thể đơn giản hơn:

• Khi lãi được tính hàng năm (n=1): Nếu lãi suất được ghép hàng năm, công thức tính lãi kép sẽ được rút gọn thành: A=P×(1+r)t Đây là trường hợp đơn giản nhất, thường gặp trong các khoản đầu tư dài hạn có kỳ hạn cố định và lãi được trả vào cuối mỗi năm.

• Khi tính lãi hàng tháng, hàng quý: Về bản chất, bạn vẫn sử dụng công thức tính lãi kép tổng quát, chỉ thay đổi giá trị của n tương ứng:

• Lãi hàng tháng: n=12

• Lãi hàng quý: n=4

• Lãi hàng nửa năm: n=2

Ví dụ so sánh tần suất ghép lãi: Giả sử bạn gửi 10.000.000 VNĐ với lãi suất 6% trong 5 năm.

• Tính lãi theo năm (n=1): A=10.000.000times(1+0.06)5approx13.382.256 VNĐ

• Tính lãi theo tháng (n=12): A=10.000.000times(1+frac0.0612)(12times5) A=10.000.000times(1+0.005)60 Aapprox10.000.000times1.348.850approx13.488.500 VNĐ

Qua ví dụ này, có thể thấy rằng cùng một số tiền gốc, cùng lãi suất và thời gian, nhưng việc ghép lãi hàng tháng mang lại số tiền cao hơn một chút so với ghép lãi hàng năm. Điều này nhấn mạnh tầm quan trọng của yếu tố n trong công thức tính lãi kép. Tần suất ghép lãi càng lớn, hiệu ứng lãi kép càng mạnh mẽ.

Công thức tính lãi suất kép (lãi suất thực tế)

Đôi khi, bạn có thể biết số tiền gốc (P), số tiền cuối cùng (A), số lần ghép lãi (n), và thời gian (t), nhưng muốn tìm ra lãi suất thực tế (r) mà khoản đầu tư của mình đã mang lại. Đây là lúc cần đến công thức tính lãi suất kép ngược lại từ công thức tổng quát.

Để tìm r, chúng ta cần biến đổi công thức tính lãi kép gốc:

A=Ptimes(1+fracrn)nt fracAP=(1+fracrn)nt (fracAP)frac1nt=1+fracrn (fracAP)frac1nt−1=fracrn r=ntimes((fracAP)frac1nt−1)

Ví dụ: Bạn đầu tư 50.000.000 VNĐ và sau 5 năm số tiền đó tăng lên thành 80.000.000 VNĐ, với lãi được ghép hàng năm (n=1). Lãi suất thực tế bạn nhận được là bao nhiêu?

• A=80.000.000 VNĐ

• P=50.000.000 VNĐ

• n=1

• t=5 năm

Áp dụng công thức tính lãi suất kép:

r=1times((frac80.000.00050.000.000)frac11times5−1) r=(1.6)frac15−1 rapprox1.09856−1 rapprox0.09856 hay 9.856%

Hiểu được công thức tính lãi suất kép (lãi suất thực tế) giúp bạn đánh giá hiệu quả của các khoản đầu tư trong quá khứ hoặc so sánh tiềm năng sinh lời của các cơ hội đầu tư khác nhau.

Cách tính lãi kép chi tiết từng bước

Việc tính lãi kép không chỉ dừng lại ở việc biết công thức tính lãi kép. Điều quan trọng là bạn phải biết cách tính lãi kép chi tiết từng bước, đặc biệt là khi muốn kiểm tra kết quả hoặc thực hiện các tính toán thủ công.

Hướng dẫn từng bước tính lãi kép

Dưới đây là các bước cụ thể để bạn tự tính lãi kép cho một khoản đầu tư:

1. Xác định các biến số:

• Số tiền gốc ban đầu (P): Khoản tiền bạn bắt đầu đầu tư hoặc gửi tiết kiệm.

• Lãi suất danh nghĩa hàng năm (r): Lãi suất được công bố, chuyển về dạng thập phân. Ví dụ: 7% = 0.07.

• Số lần ghép lãi trong một năm (n): Tần suất lãi được cộng vào vốn gốc.

• Hàng năm: n=1

• Nửa năm: n=2

• Hàng quý: n=4

• Hàng tháng: n=12

• Hàng ngày: n=365

• Số năm đầu tư (t): Tổng thời gian bạn dự định để khoản tiền sinh lời.

2. Tính toán phần lãi suất theo kỳ (r/n): Chia lãi suất danh nghĩa hàng năm cho số lần ghép lãi trong một năm để biết lãi suất áp dụng cho mỗi kỳ.

3. Tính toán tổng số kỳ ghép lãi (nt): Nhân số lần ghép lãi trong một năm với tổng số năm để ra tổng số kỳ mà tiền lãi được cộng dồn.

4. Tính toán giá trị của (1+r/n): Cộng 1 với kết quả từ bước 2.

5. Lũy thừa giá trị vừa tìm được lên số mũ (nt): Tính (1+r/n)nt. Đây là yếu tố tăng trưởng chính của lãi kép.

6. Nhân kết quả với số tiền gốc ban đầu (P): A=Ptimes(1+fracrn)nt. Kết quả cuối cùng chính là tổng số tiền bạn nhận được, bao gồm cả vốn gốc và lãi.

Ví dụ cụ thể với số liệu thực tế

Hãy áp dụng các bước trên để tính lãi kép cho ví dụ sau: Bạn gửi 10.000.000 VNĐ vào tài khoản tiết kiệm với lãi suất 8% mỗi năm, lãi được ghép theo tháng trong 3 năm.

• Bước 1: Xác định biến số
  
  

• P=10.000.000 VNĐ

• r=0.08

• n=12 (theo tháng)

• t=3 năm

• Bước 2: Tính lãi suất theo kỳ (r/n) 0.08/12approx0.00666667

• Bước 3: Tính tổng số kỳ ghép lãi (nt) 12times3=36 kỳ

• Bước 4: Tính (1+r/n) 1+0.00666667=1.00666667

• Bước 5: Lũy thừa giá trị lên số mũ (nt) (1.00666667)36approx1.270237

• Bước 6: Nhân với số tiền gốc (P) A=10.000.000times1.270237approx12.702.370 VNĐ

Bảng minh họa kết quả từng năm (hoặc từng kỳ tính lãi): Để thấy rõ sự tăng trưởng của lãi kép, hãy xem bảng minh họa cho ví dụ trên theo từng năm:

(Lưu ý: Các số liệu trong bảng được làm tròn để dễ hình dung, và lãi suất 8% được tính trên cơ sở ghép lãi hàng tháng, sau đó quy đổi ra hiệu quả thực tế hàng năm xấp xỉ 8.3%).

Lưu ý về tần suất tính lãi và ảnh hưởng đến kết quả

Như đã đề cập, tần suất ghép lãi (n) là một yếu tố quan trọng ảnh hưởng đến số tiền cuối cùng bạn nhận được. Lãi được ghép càng thường xuyên (ví dụ: hàng tháng thay vì hàng năm), số tiền cuối cùng sẽ càng lớn hơn. Điều này là do lãi được cộng vào vốn gốc sớm hơn, và sau đó chính khoản lãi đó lại tiếp tục sinh lãi, tạo ra hiệu ứng tăng trưởng mạnh mẽ hơn.

Khi bạn so sánh các sản phẩm tài chính, đừng chỉ nhìn vào lãi suất danh nghĩa mà hãy hỏi rõ về tần suất ghép lãi để có cái nhìn chính xác nhất về tiềm năng sinh lời của khoản đầu tư.

Biểu đồ so sánh tăng trưởng lãi đơn và lãi kép

Công cụ và phương pháp hỗ trợ tính lãi kép

Trong kỷ nguyên số, việc tính lãi kép không còn quá phức tạp nhờ sự hỗ trợ của các công cụ và phần mềm. Nắm vững công thức tính lãi kép là cần thiết, nhưng biết cách sử dụng các công cụ này sẽ giúp bạn tiết kiệm thời gian và đảm bảo độ chính xác.

Công cụ tính lãi kép online

Các công cụ tính lãi kép trực tuyến là giải pháp nhanh chóng và tiện lợi cho bất kỳ ai muốn ước tính khoản tiền trong tương lai của mình. Chúng thường có giao diện thân thiện, dễ sử dụng.

Một số website/ứng dụng phổ biến:

• Ngân hàng và tổ chức tài chính: Nhiều ngân hàng tại Việt Nam (ví dụ: Vietcombank, Techcombank, VPBank) cung cấp công cụ tính lãi kép trực tiếp trên website của họ để hỗ trợ khách hàng ước tính tiền gửi tiết kiệm.

• Các trang web tài chính cá nhân: Các trang web như The Calculator Site, Investopedia, hay Calculator.net đều có các công cụ tính lãi kép mạnh mẽ và đa năng, cho phép bạn điều chỉnh nhiều biến số khác nhau.

• Ứng dụng di động: Có rất nhiều ứng dụng di động miễn phí hoặc trả phí trên App Store (iOS) và Google Play Store (Android) được thiết kế riêng để tính lãi kép và quản lý tài chính cá nhân.

Hướng dẫn sử dụng chung:

1. Truy cập công cụ: Mở website hoặc ứng dụng tính lãi kép bạn muốn sử dụng.

2. Nhập dữ liệu: Bạn sẽ thấy các trường để nhập:

• Số tiền gốc ban đầu (Initial Deposit/Principal)

• Lãi suất hàng năm (Annual Interest Rate)

• Tần suất ghép lãi (Compounding Frequency: Annually, Monthly, Quarterly, Daily, etc.)

• Thời gian đầu tư (Investment Period/Years)

• (Tùy chọn) Khoản bổ sung định kỳ (Regular Contributions): Một số công cụ cho phép bạn nhập số tiền gửi thêm hàng tháng/quý.

3. Xem kết quả: Sau khi nhập đủ thông tin, công cụ sẽ tự động tính toán và hiển thị tổng số tiền cuối cùng, tổng lãi kiếm được, và đôi khi là biểu đồ tăng trưởng.

Cách sử dụng Excel để tính lãi kép

Microsoft Excel là một công cụ cực kỳ linh hoạt và mạnh mẽ để tính lãi kép, đặc biệt nếu bạn cần thực hiện các phân tích phức tạp hơn hoặc xây dựng các mô hình tài chính tùy chỉnh.

Công thức Excel cơ bản: Bạn có thể áp dụng trực tiếp công thức tính lãi kép vào Excel: =P*(1+r/n)^(n*t)

Hoặc sử dụng hàm FV (Future Value) tích hợp sẵn: =FV(rate, nper, pmt, [pv], [type])

Trong đó:

• rate: Lãi suất theo kỳ (r/n).

• nper: Tổng số kỳ (nt).

• pmt: Khoản thanh toán định kỳ (Payment). Đối với tính lãi kép đơn thuần từ một khoản gốc, pmt là 0. Nếu bạn có gửi thêm định kỳ, hãy nhập giá trị này.

• pv: Giá trị hiện tại (Present Value) hay số tiền gốc ban đầu (P). Nhập giá trị âm để biểu thị dòng tiền ra (khoản đầu tư ban đầu).

• [type]: Tùy chọn, xác định thời điểm thanh toán (0 cho cuối kỳ, 1 cho đầu kỳ). Thường là 0.

Ví dụ cụ thể từng bước sử dụng hàm FV trong Excel:

Giả sử bạn gửi 10.000.000 VNĐ, lãi suất 8% mỗi năm, lãi ghép theo tháng, trong 3 năm.

1. Mở một bảng tính Excel mới.

2. Nhập các giá trị vào các ô riêng biệt để dễ quản lý:

• A1: P (Vốn gốc) = 10,000,000

• A2: r (Lãi suất năm) = 0.08

• A3: n (Số lần ghép lãi/năm) = 12

• A4: t (Số năm) = 3

3. Tại ô mà bạn muốn hiển thị kết quả (ví dụ: A5), nhập công thức FV: =FV(A2/A3, A3*A4, 0, -A1)

• A2/A3 tương ứng với rate (0.08/12).

• A3*A4 tương ứng với nper ($12\*3$).

• 0 là pmt (không có khoản gửi thêm định kỳ).

• -A1 là pv (10.000.000 VNĐ được nhập âm vì đây là tiền bạn bỏ ra ban đầu).

4. Nhấn Enter. Excel sẽ trả về kết quả xấp xỉ 12.702.370 VNĐ (có thể có sự khác biệt nhỏ về làm tròn).

Mẹo và lưu ý khi sử dụng công cụ tính lãi kép

Để đảm bảo tính chính xác khi sử dụng các công cụ tính lãi kép, hãy lưu ý những điểm sau:

• Đơn vị lãi suất và tần suất tính lãi: Luôn đảm bảo rằng bạn nhập đúng đơn vị cho lãi suất (thường là thập phân) và chọn đúng tần suất ghép lãi (n) cho phù hợp với thông tin bạn có. Sai sót nhỏ ở đây có thể dẫn đến kết quả sai lệch lớn.

• Kiểm tra kết quả với công thức tay: Đối với các tính toán quan trọng hoặc khi mới bắt đầu sử dụng công cụ, hãy thử tính lãi kép thủ công với một ví dụ đơn giản và so sánh với kết quả từ công cụ. Điều này giúp bạn kiểm tra xem mình đã hiểu và nhập liệu đúng chưa.

• Hiểu rõ các biến số: Không chỉ biết cách nhập số liệu, mà bạn còn cần hiểu ý nghĩa của từng biến số trong công thức tính lãi kép và cách chúng ảnh hưởng đến kết quả cuối cùng.

• Lưu ý đến các khoản phí hoặc thuế: Các công cụ tính lãi kép thường chỉ đưa ra số liệu thô. Trong thực tế, bạn cần tính đến các khoản phí quản lý tài khoản, phí giao dịch (nếu có) và thuế thu nhập từ lãi để có cái nhìn toàn diện về lợi nhuận ròng.

Chồng đồng tiền tăng dần qua từng mốc lịch hàng tháng

Câu hỏi thường gặp (FAQs)

Lãi kép được tính thế nào khi gửi tiết kiệm có kỳ hạn?

Khi gửi tiết kiệm có kỳ hạn, lãi kép thường được tính dựa trên nguyên tắc lãi suất được nhập gốc sau mỗi kỳ hạn gửi (ví dụ: 6 tháng, 12 tháng). Khi đến hạn, tiền lãi của kỳ đó sẽ được cộng vào vốn gốc, và toàn bộ số tiền này sẽ trở thành vốn gốc mới cho kỳ hạn tiếp theo nếu bạn tiếp tục tái tục. Công thức tính lãi kép tổng quát vẫn được áp dụng, với n bằng 1 nếu bạn chỉ tái tục theo năm, hoặc bằng số kỳ đáo hạn trong một năm.

Tần suất tính lãi ảnh hưởng ra sao đến số tiền cuối cùng?

Tần suất tính lãi (n trong công thức tính lãi kép) ảnh hưởng trực tiếp đến số tiền cuối cùng. Lãi được ghép càng thường xuyên (ví dụ: hàng tháng thay vì hàng năm), số tiền cuối cùng bạn nhận được sẽ càng lớn. Điều này là do lãi được cộng vào gốc sớm hơn, và sau đó chính khoản lãi đó lại tiếp tục sinh lãi.

Cách tính khi lãi suất thay đổi theo thời gian?

Khi lãi suất thay đổi theo thời gian, bạn không thể áp dụng một lần công thức tính lãi kép duy nhất cho toàn bộ giai đoạn. Thay vào đó, bạn cần tính lãi kép cho từng giai đoạn có lãi suất cố định, sau đó lấy tổng số tiền cuối kỳ của giai đoạn trước làm vốn gốc cho giai đoạn kế tiếp.

Ví dụ: 3 năm đầu lãi suất 6%, 2 năm sau lãi suất 7%.

• Tính tổng tiền sau 3 năm đầu với lãi suất 6%.

• Lấy kết quả đó làm vốn gốc để tính tiếp cho 2 năm sau với lãi suất 7%.

Công cụ tính lãi kép chính xác nào?

Các công cụ tính lãi kép online của các ngân hàng uy tín, các trang web tài chính như Investopedia, Calculator.net, hoặc sử dụng hàm FV trong Microsoft Excel đều cho kết quả chính xác. Điều quan trọng là bạn phải nhập đúng và đủ các biến số vào công cụ.

Lãi kép có phải cách tốt nhất để tăng trưởng tài sản?

Lãi kép là một nguyên lý mạnh mẽ và là một trong những cách hiệu quả nhất để tăng trưởng tài sản trong dài hạn. Tuy nhiên, nó không phải là cách duy nhất và cũng không hoàn toàn không có rủi ro. Việc tăng trưởng tài sản tốt nhất thường là sự kết hợp giữa việc tận dụng lãi kép (thông qua tiết kiệm, đầu tư tái đầu tư lợi nhuận) và đa dạng hóa danh mục đầu tư, quản lý rủi ro, và tìm kiếm các cơ hội đầu tư phù hợp với mục tiêu tài chính cá nhân.

Hãy nhớ rằng, sức mạnh thực sự của lãi kép nằm ở sự kiên nhẫn và tính kỷ luật trong việc tái đầu tư lợi nhuận. Đừng để lỡ mất cơ hội làm giàu từ chính số tiền bạn đang có. Áp dụng những kiến thức này ngay hôm nay để quản lý tài chính cá nhân hiệu quả và đạt được mục tiêu thịnh vượng trong tương lai! HVA xin chúc bạn luôn thành công!